Unlocking 3D Games: A Math Wizard’s Guide

Dive into the fascinating intersection of mathematics and 3D programming with Aaron’s insightful blog, as he unveils the essential role of maths in creating realistic 3D environments in computer games, challenging the conventional focus on programming skills alone.

Firstly, what do I mean by 3D programming? A brief Introduction…

For this blog, when I discuss 3D programming, I am talking about the development of 3D computer games and how to create a 3D environment that will give the illusion of reality on a 2D screen.

Surprisingly, though I may be discussing 3D “Programming”, the programming element of this is not the most important part, but instead the mathematics are the most essential elements of 3D games.

The programming part of 3D games mostly involves creating the images, this can usually be done by using a draw function, or the equivalent of the pen function on scratch, but it is the mathematic calculations behind where to draw, and how big to draw that make 3D games and programming so rare in school projects and online in general. It is also not a concept many can understand easily, as this is usually not taught in an average school computer science class.

Another way that people can access 3D game development is by using a library. Libraries are collections of pre-written code that allow you to be able to perform specific tasks (according to the code), which in this case could be 3D coding calculations. However, I believe that simply using a library (or pre-written code) in order to do these calculations, does not end up helping you understand how and why the code works, but simply teaches you how to use a piece of pre-written code. Furthermore, these libraries sometimes cannot be transferred through different coding languages, meaning that you will not be able to transfer these skills and knowledge to other languages easily.

Instead of using these libraries, I believe that understanding the concepts behind 3D game programming will help develop not only your understanding of 3D games, but develop the vast theories of mathematics, and allow you to add on to on these ideas.

Now, to start.

The Game

The game I will be trying to teach you here on my blog is a 3D room as shown below:

The elements of a basic room are quite simple, all we need are walls to show where in a room we are.

The first boundary we reach is generating our walls.

I use pygame, which is a game development library (there are very likely similar versions for other languages), that I use specifically so that I can open a game environment (This does not include any 3D calculations, I have used this library simply to create visuals).

To create images on pygame I can use the draw() function (the equivalent of the pen function on scratch). This creates a rectangle in which I can modify the height, the width, and the colour of said rectangle. However, this can only make a 2D shape (rectangle), and this is a problem; because this restricts us to one image of a wall, which in our world looks different on every angle you see it.

This means we have to use multiple of these rectangles and combine them into a layered wall. This allows us to be able to manipulate the shaping of the walls, so that we can allow our avatar (yourself) to change angle accurately.

Now to the calculations.

Calculations:

There are 2 types of calculation you will need to use in 3D games, these are:

• Positions of objects in our 3D world (how far they seem to be)
• Positions of objects on our monitor (where they actually are on your screen)

For simplicity I have called these 2 stages:

• Object Calculations (relating to object position)
• Screen Calculations (relating to screen)

Object calculations:

The object calculations we need are the following:

• Distance from avatar (Yourself)
• On what angle do they appear (avatar’s angle)

How do we do this?

The easiest way to understand the objects’ location, is by using a grid, similar to how maps work. To make this grid we will use a concept in maths called a matrix. This is basically just a grid made by lists in a list as I shown below:

This gives us an easy to edit diagram of our entire room if we assume that 0 as a value means no wall and 1 or above means a wall.

Sidenote: In the matrix above I have used the different numbers in the matrix to represent different colours for the walls as you can see in the example above.

Distance

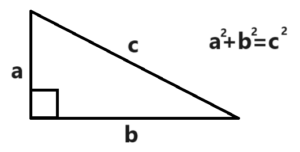
Now to find the distance between 2 objects we can use Pythagoras theorem (diagram below) which is (a^2 + b^2 = c^2), in our example, because of our grid format we can calculate our change in x and change in y by finding our difference in grid positions. We can then use them as (a) and (b) in the formula because the x and y grid format are at 90 degrees to each other. Using this formula, we can measure the distance by calculating c. We can do this by rooting (a^2 + b^2) to find the value of c.

Side note: in this room we will be only making 1 floor but if you make several layers in your matrix, you can use 3D Pythagoras to calculate the distance (I have linked some information on this below).

Angle

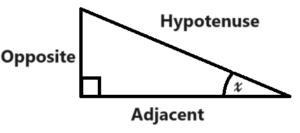
In a right-angle triangle, there are a few ratios that can link the distances of sides with the angle of the triangle. These ratios are Sine, Cosine and Tangent.

The ratios are:

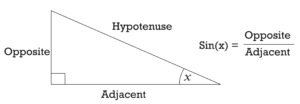
Sin(x) = opposite / hypotenuse

Cos(x) = adjacent / hypotenuse

Tan(x) = opposite / adjacent

The formulas above reference the triangle shown above, these use (x) as the angle, usually this is presented with theta (θ) but for simplicity I believe x will be easier to understand.

Now we know the formula, we need to extract x (or the angle), and to do so, we will have to balance out the equation. Similarly to how multiplication is the opposite of division, arcsine is the opposite of sine, arccosine is the opposite of cosine and arctangent is the opposite of tangent. Because of this, to extract the x we need to reverse the function at the beginning as shown below:

• Sin(x) = opposite / hypotenuse
• Asin (Sin(x)) = Asin (opposite / hypotenuse)
• x = Asin (opposite / hypotenuse)

• Cos(x) = adjacent / hypotenuse
• Acos (Cos(x)) = Acos (adjacent / hypotenuse)
• x = Acos(adjacent / hypotenuse)

• Tan(x) = opposite / adjacent
• Atan (Tan(x)) = Atan (opposite / adjacent)
• x = Atan (opposite / adjacent)

With any of these formulas we can now calculate the angle on which they are on.

Remember that for these games we may need to calculate both the angle going up and down, and the angle going horizontally. To calculate these different values, we can imagine 2 different triangles. For both these triangles our focus is to on inserting information into the equations. For a calculation for the horizontal angle, we can use:

Atan (opposite / adjacent)

And with this, we can insert our opposite as the change in x, and the adjacent is the change in to make:

Atan (x/y)

As well as this, you can use the same formula for the vertical angle, but instead of using the change in y or change in x as the opposite or adjacent, you should use the change in z instead to account for the 3^rd dimension.

Screen Calculations:

Positioning

The screen calculations are one of the most complex parts of this process, because of its non-obvious concepts.

It is in this section in which we start to use our walls.

The things we need to transfer our object (wall) calculations to are the following:

• x position on screen
• y position on screen
• size

To understand how we can put our images in the right position, we need to calculate the difference in x and y position from our avatar to the object.

To calculate this accurately, we can once again use trigonometry as seen below:

The x position and y position are both, the perpendicular (right-angle) distance from the centre of our view (the mid-point of the screen).

Because the x and y position are the perpendicular distance (right-angle), we can use a right-angle triangle to represent this information this triangle to be able to calculate the distance.

To do this we can use the distance we calculated earlier in the form of the hypotenuse and, the angle we have calculated as the value x usually (θ) (vertical angle for y position, horizontal angle for x position), to represent our right-angle triangle.

Due to trigonometry, we know there are certain ratios between the angles in a right-angle triangle, and the lengths of the sides in the same triangle.

These ratios are:

• Sin(x) = opposite / hypotenuse
• Cos(x) = adjacent / hypotenuse
• Tan(x) = opposite / adjacent

Using these ratios, we can calculate the specific value for the opposite.

This allows us to use the formula:

Sin(x) = opposite / hypotenuse

(hypotenuse is just the distance)

As I said earlier, the value Sin(x) is the ratio of opposite/hypotenuse. In order to calculate the value of only the opposite, we can rearrange the formula like so:

Sin(x) * hypotenuse = opposite

Now we have the opposite (or distance from centre) we can now calculate the x position of our object.

Now because the opposite is the distance from the centre of vision, we can use:

Screen midpoint + opposite = x position

With the formula I have shown above, we can accurately calculate the x position for our objects, but this doesn’t only work for x position, but y position also. To calculate the y-position we can use the angle upwards, to calculate the vertical opposite instead of the horizontal opposite.

Size

Now to calculate the size of our objects we can use the perspective calculation, which is:

Size = Original size / distance

In this the original size can be a variable you assign and is the biggest size possible for your object, or the size of the object if you are next to it.

An issue you may realise when coding this is 0 division error. This happens when you divide something by 0 (which cannot be calculated), this leads to the Zero Division error which can close or glitch your entire game. To counter this you can make an exception which says that:

if distance == 0 then:

size = Original size

This will make sure that when the distance is 0 then the size is at its maximum.

Conclusion

Finally, after all the questioning in school, we have found a useful function for trigonometry!

In this blog, I hope to have shown you the theories we can use to be able to understand the 3D world we live in.

Currently, using these mathematical models and theories, I have been able to make my own version of these 3D games which I have shown in one of the pictures above. This game is a less of a game and more of an interactive area where you can discover the rooms I have designed inside, but I hope that in time I will be able to find myself developing large scale 3D games to show others and just for my own enjoyment.

However, in the end, I want you (the reader) to be able to not only understand the theories surrounding the 3D games but give you the encouragement to discover this field of learning for yourself.

To find out more about trigonometry, you can use websites such as Corbett maths, or maths and BBC Bitesize to learn more about trigonometry. As for the applications in games, I used my own problem solving and a lot of trial and error to get to this stage in 3D programming, and I am sure that you can all do the same by applying logical reasoning, maths, and a lot of trial and error to these situations.

Thank you for reading.

Links:

Trigonometry videos:

https://corbettmaths.com/2018/04/25/trigonometry-videos/

Trigonometry:

https://www.bbc.co.uk/bitesize/guides/ztj6y4j/revision/1

3D Trigonometry:

Trigonometry in 3 dimensions – Higher – Trigonometry – AQA – GCSE Maths Revision – AQA – BBC Bitesize