In today’s world, protecting individual privacy is more important than ever. In this post, Dylan explores what differential privacy is, why it matters, and how it’s shaping the future of data security. Read on to find out more.
It’s fair to say that everything you do online counts as data – everything you buy, search or review. It’s all data. Companies want your data because it can help them create more targeted ads or develop products that are more suited to your preferences. This can generate more sales. This doesn’t sound too bad…. but what about data that’s more private? For example, data about your daily journey or location. Many people feel uncomfortable about having so little privacy from companies, and this can raise serious concerns.
So, how can companies collect data while still letting users remain anonymous?
In the past, there have been a few methods that companies have used to help users stay anonymous. One is data anonymisation, where data is gathered as usual but the user identifier is simply erased. Another method is k-anonymity, where data is grouped to be less specific. For example, if someone was 36 years old, their age may be displayed as 35-40 in a dataset rather than 36.
However, both of these methods have turned out to be ineffective as they are still vulnerable to linkage attacks (Borealis AI, 2023). A famous example happened in 2006, when Netflix hosted a competition called “The Netflix Prize”. They provided contestants with huge datasets consisting of hundreds of thousands of reviews. The aim of the competition was to generate an algorithm that would be able to best predict user ratings from the given dataset. The data given was said to be “anonymous” but some computer scientists later found out which reviews belonged to which people by comparing the data from the dataset to a separate dataset from IMDB. This is a classic example of a linkage attack is (Simply Explained, 2018).
This calls for a new method of anonymisation… Differential Privacy!
What is Differential Privacy?
Differential privacy is a method used to create “noise” within a dataset by randomising the data while still allowing the data to be understood by a company. The company can still extract information from the data despite it being randomised because the proportions in the data will still be relatively similar. The data is now anonymised because you cannot be sure that the data under a user may be correct or incorrect. This could allow companies to understand what proportions of people like a product without knowing who specifically likes the product.
Here is the equation for pure differential privacy (where there is no privacy leakage):
Where:
- M() is a randomising function
- D1 and D2 are neighbouring datasets
- ε is the privacy parameter
To break this down: the probability of picking the same thing from two neighbouring datasets, which have gone through randomisation, is less than e to the power of epsilon.
What’s a neighbouring dataset?
Two datasets are classed as neighbouring if they differ only by one random element.
D1 = [X1,…Xi-1, Xi, Xi+1…Xn]
D2 = [X1,…Xi-1, Xi’, Xi+1…Xn]
The epsilon is the privacy parameter. This can be controlled to maintain trade-off between privacy and accuracy. Higher values of epsilon increase the accuracy of the data but lower the privacy of the data – accuracy of the data being how close the new dataset is to the dataset before, when it was untouched (Aitsam, 2022)
There are many randomisation functions used which can be very complex to understand.
Randomised Response Mechanism
This is great for simple ‘yes’ or ‘no’ questions. A person, after being asked a question, flips a coin.
- If the person gets heads, they flip another coin:
- Heads again = They lie and say the opposite answer to their real answer.
- Tails = They answer with the truth.
- If the first coin is tails, they flip another coin and regardless of the outcome they always tell the truth.
The decision between truth or lie for either heads or tails can be personalised, meaning that the person asking the question won’t know if they’re telling the truth or not – making the data anonymous.
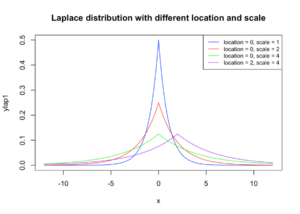
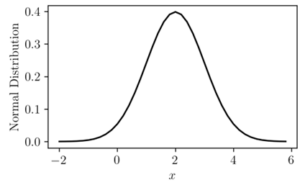
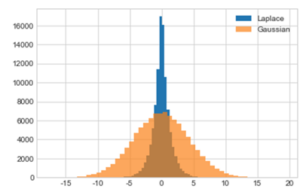
Laplace and Gaussian Mechanisms both act like random number generators while utilising the Laplace distribution (figure 1) and the Gaussian distribution (figure 2) respectively. As shown in figure 3, the Laplace distribution adds a lot more randomness to data than Gaussian (Cook, 2018).
Figure 1
Figure 2
Figure 3
The differential privacy shown above is called ‘pure differential privacy’. The equation above can be written in the form:
Pr[M(D1)∈S]≤e^ε Pr[M(D2)∈S]
If we add delta to this equation…
Pr[M(D1)∈S]≤e^ε Pr[M(D2)∈S]+δ
Where delta is the probability of privacy leakage, we get (ε, δ)-differential privacy which takes into account the probability of privacy leakage. In pure differential privacy, delta is set to 0.
Differential privacy is already being used in the real world by large corporations like Google and Apple – but things get a lot more complicated when used on a large scale. This method is also not very helpful with smaller datasets, hence why it’s mainly used by large corporations.
However, despite its complexity, differential privacy is one of the best methods to ensure anonymity and it has shown that people are more likely to give more truthful answers when kept anonymous. One last benefit of this method is that it’s backed by strong mathematics, making it easier to prove anonymity.
Bibliography
Aitsam, M. (2022) Differential Privacy Made Easy. https://arxiv.org/pdf/2201.00099.
Borealis AI (2023) Tutorial #12: Differential Privacy i: Introduction – RBC Borealis. https://rbcborealis.com/research-blogs/tutorial-12-differential-privacy-i-introduction/.
Cook, J. (2018) Generating Laplace distributed random values. https://dzone.com/articles/generating-laplace-distributed-random-values#:~:text=Although%20it%27s%20simple%20to%20generate%20Laplacian.
Dwork, C. et al. (no date) Differential privacy. https://www.stat.cmu.edu/~larry/=sml/diffpriv.pdf.
Jinshuo Dong, Aaron Roth, Weijie J. Su, Gaussian Differential Privacy, Journal of the Royal Statistical Society Series B: Statistical Methodology, Volume 84, Issue 1, February 2022, Pages 3–37
Simply Explained (2018) Differential privacy – simply explained. https://www.youtube.com/watch?v=gI0wk1CXlsQ.
Wikipedia contributors (2024) Differential privacy. https://en.wikipedia.org/wiki/Differential_privacy.
Wikipedia contributors (2024) Additive noise differential privacy mechanisms. https://en.wikipedia.org/wiki/Additive_noise_differential_privacy_mechanisms.
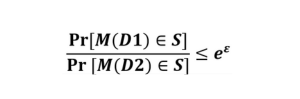
Dylan is a Year 12 student from Manchester currently working towards his gold award. His main interests are computer science and maths. He is hoping to work in computer science in the future.
