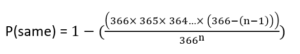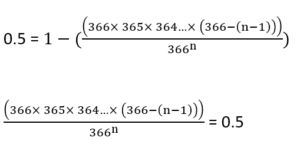The Birthday Paradox is one of those fascinating mathematical quirks that seems almost too good to be true. In her post, Valerie explores the probability behind the paradox, why it works, and what it reveals about randomness and probability in everyday life. Read on to learn more.
What Is the Birthday Paradox?
The Birthday Paradox is a mathematical problem which illustrates the (perhaps counter intuitive) probability of two people sharing the same birthday. This paradox states that in a room of just 23 people, there is a 50% chance that two of them will share the same birthday.
This statement might seem strange or unreasonable at first, perhaps because initially we might think that we need around 180 people for there to be a 50% chance of two people sharing the same birthday. However, by using probability, which by definition is the likelihood of something happening or being true (Probability, Cambridge English Dictionary), we can calculate a result that is quite surprising.
Understanding the Birthday Paradox
Take the probability of any two people in the same room sharing the same birthday as P(same).
Take the probability of any people in the room not sharing a birthday as P(not).
As there are only two possible outcomes in our scenario, we know that adding the probabilities P(same) and P(not) must add up to 100%.
Therefore: P(same) + P(not) = 1
Calculating the Probability Step by Step
So, what is then the probability of two people not sharing a birthday?
Let’s investigate the probabilities when we have a sample size of two people.
The first person could have a birthday on any date of the year, so the probability is
366⁄366
The probability of the second person not sharing the same birthday is
365⁄366
To find the probability that these two people do not share the same birthday:
366⁄366 ×
365⁄366 ≈ 0.997 or 99.7%
Therefore, the probability of two people sharing the same birthday is 1 – 0.997 = 0.00273 or 0.273%
What If There Are Three or More People?
What about the probability of sharing a birthday when we have a sample size of three people?
The probability of these three people not sharing the same birthday would be
366⁄366 ×
365⁄366 × 364⁄366 = 0.992 or 99.2%.
Therefore, the probability of any two of the three people sharing the same birthday is 1 – 0.992 = 0.00818 or 0.818%.
What about the probability of sharing a birthday when we have a sample size of four people?
The probability of these four people not sharing the same birthday would be 366⁄366 ×
365⁄366 × 364⁄366 × 363⁄366 = 0.984 or 98.4%.
Therefore, the probability of any two of the four people sharing the same birthday is 1 – 0.984 = 0.0163 or 1.63%.
What Do These Results Show?
From our calculations above, we can observe that the probability increases rapidly as the number of people increases. Therefore, we can infer that as the sample size increases, the number of unique birthday combinations decreases, thus increasing the probability of any two people sharing a birthday.
The General Formula
We can create an equation that illustrates the number of people needed for there to be a 50% chance of any two people sharing a birthday.
Let n be the number of people needed for the statement above to be true. (www.rigb.org, n.d.)
When the value of P(same) > P(not), this is when there is a >50% chance of any two people sharing a birthday.
We can rearrange the equation as follows:
When we solve this problem, this n value occurs at 23, giving a probability of 0.506 or 50.6%.
References
-
“Probability” Dictionary.cambridge.org: https://dictionary.cambridge.org/dictionary/english/probability
-
Royal Institution: https://www.rigb.org/explore-science/explore/blog/birthday-paradox
Valerie is in year 12 and working towards a Bronze Youth STEMM Award. Her main interests are nature, puzzle solving, maths and science
